论文
MNA本科毕业论文写作指南:选题到答辩全流程解析
写mna本科毕业论文是不是让你头大?
选题没方向,文献看不懂,数据不会分析?
你不是一个人!很多同学都在为这个发愁。
现在要求越来越高,竞争越来越激烈。
这不仅是写论文的问题,更考验你的研究能力、逻辑思维和时间管理。
那到底该怎么办呢?
别急,这里有一份清晰实用的指南。
从选题到答辩,一步步教你写出高质量mna本科毕业论文。
mna本科毕业论文写作指南
写作准备与方向确定
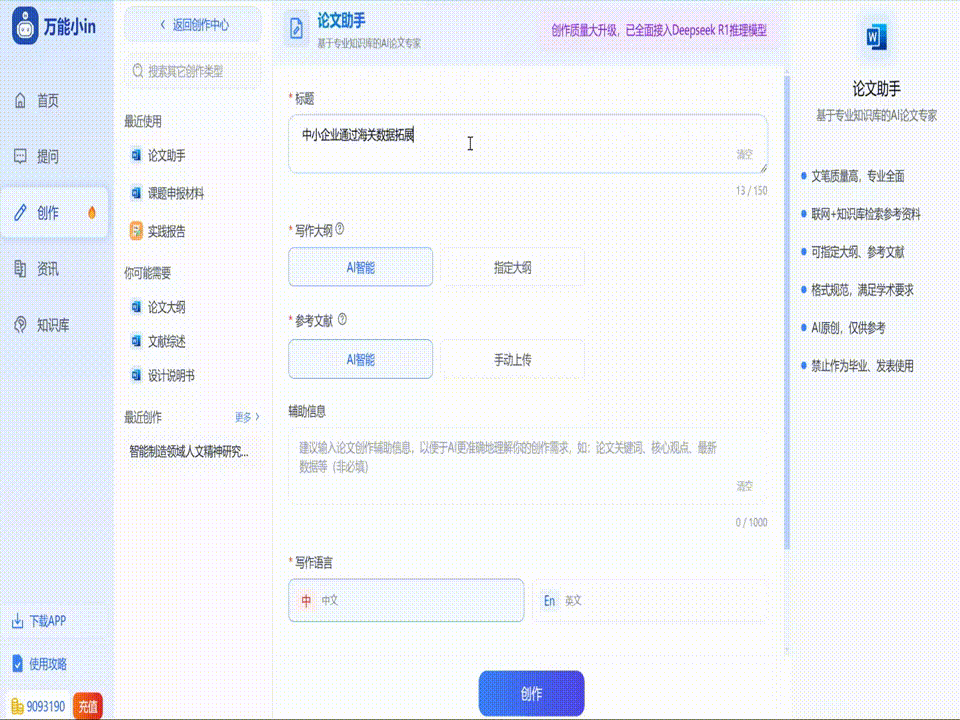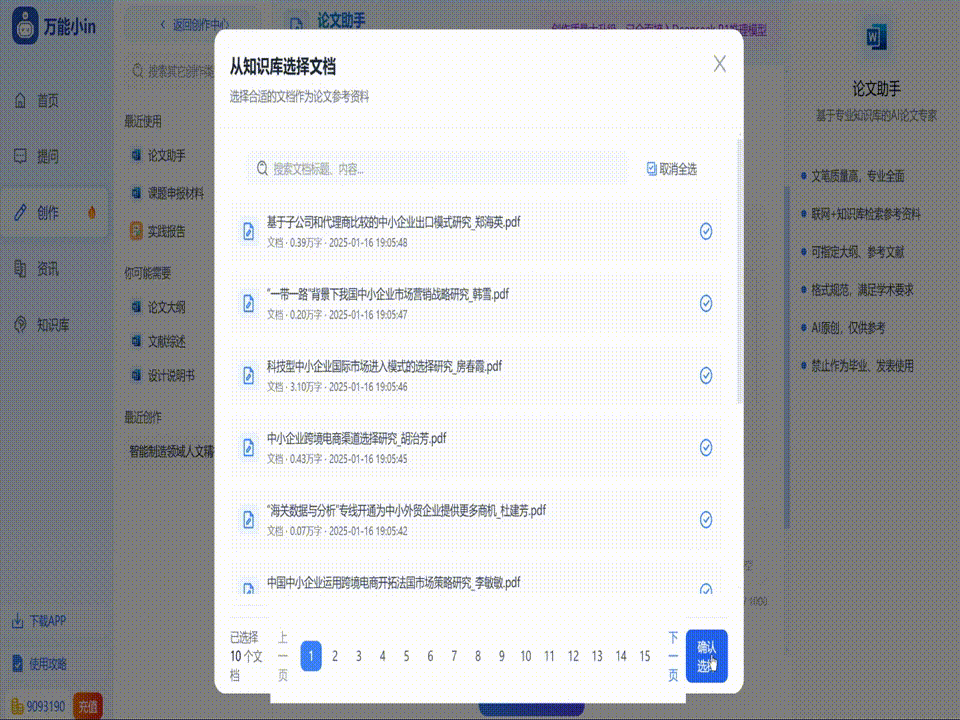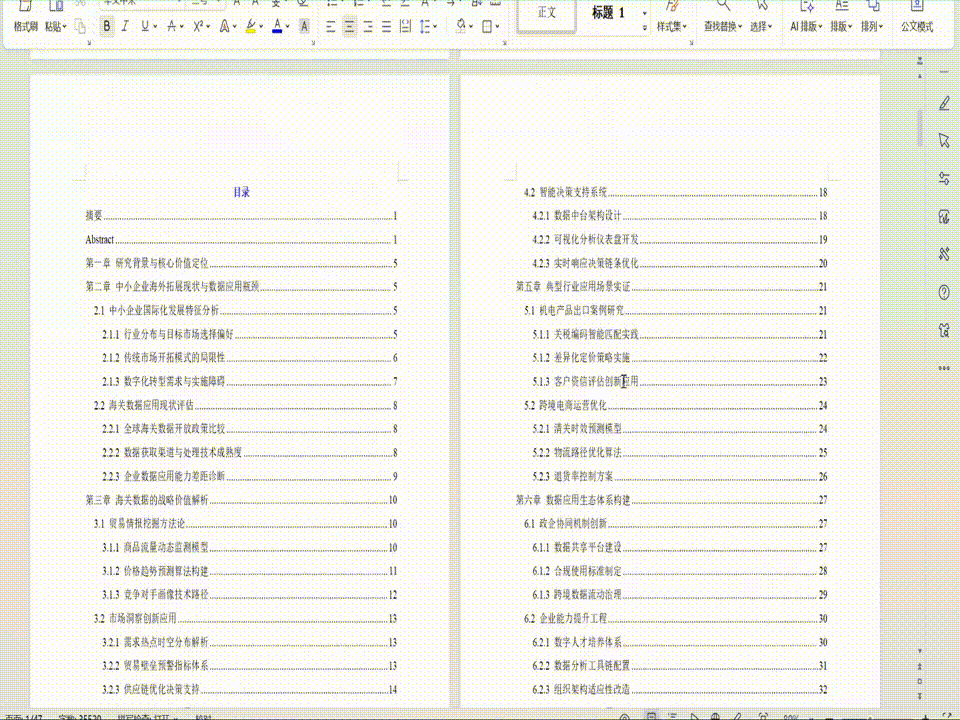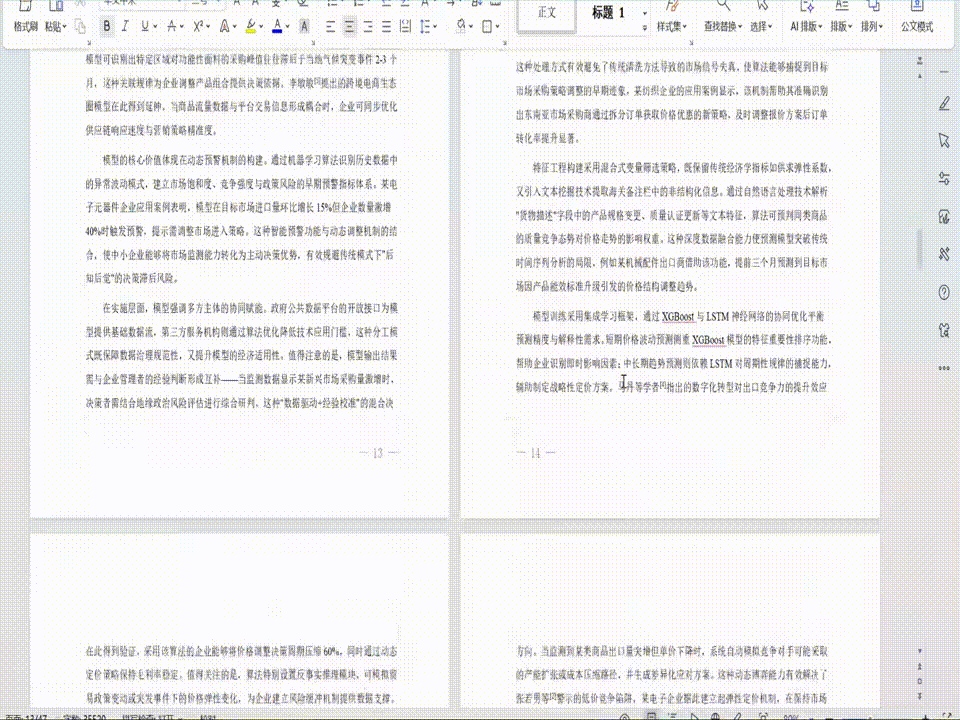
在开始写作前,首先需要明确mna本科毕业论文的主题和研究方向。mna通常指管理网络与自动化,选题应结合当前技术发展趋势或实际应用需求。建议从以下方面准备:
- 选题原则:选择具有学术价值或实践意义的课题,如智能管理系统的优化、自动化技术的应用案例等。
- 资料收集:查阅国内外相关文献,重点关注近5年的研究成果,整理关键数据和理论框架。
- 结构规划:确定论文的基本框架,包括摘要、引言、文献综述、方法论、结果分析、结论等部分。
- 目标受众:明确论文的读者群体,如学术导师、行业专家或技术开发者,调整写作风格和深度。
写作思路与技巧
写作过程中需注重逻辑性和学术性,以下为具体指导:
- 论述展开:采用问题导向式结构,先提出研究问题,再通过理论分析和实验数据逐步解答。
- 段落安排:每个段落聚焦一个子主题,使用主题句开头,辅以证据或案例支撑。
- 思想表达:在文献综述和方法论部分体现批判性思维,对比不同学者的观点并提出自己的见解。
- 语言运用:使用学术化表达,避免口语化,专业术语需准确定义。图表应清晰标注来源。
核心观点与创新表达
mna领域的论文应突出技术应用或理论创新,以下为可选方向:
- 关键技术:分析特定算法(如深度学习)在管理自动化中的优化效果。
- 案例研究:选取企业实施mna系统的真实案例,评估其经济效益或技术瓶颈。
- 跨学科视角:探讨mna与物联网、大数据等技术的融合可能性。
- 创新建议:基于研究发现,提出改进现有系统的新思路或未解决问题。
修改完善与后续应用
完成初稿后需系统化优化:
- 逻辑检查:确保每个结论都有对应论据支撑,消除前后矛盾。
- 语言润色:修正语法错误,统一术语使用,精简冗余表述。
- 答辩准备:制作简洁的PPT,重点突出研究方法和创新点,预判可能的技术性质疑。
- 成果延伸:可将核心内容改写为期刊论文或会议报告,或作为项目申报书的基础材料。
常见误区与注意事项
写作中需警惕以下问题:
- 选题过空:避免”mna技术概述”等宽泛主题,应聚焦具体问题。
- 数据不足:实验样本量过小或对比组缺失会导致结论可信度降低。
- 格式错误:参考文献标注不规范、图表编号混乱等细节问题。
- 创新模糊:需明确区分他人成果与自身贡献,避免夸大研究价值。
不想看写作指南?可以试试万能小in AI论文助手,一键生成论文初稿,高效省时!
那么轻松就能完成一篇论文初稿,快来体验一下吧~~无需担心论文查重、格式等问题,毕竟万能小in AI写论文是专业的。
面对mna本科毕业论文的压力?别担心,AI写作工具能帮你轻松应对!无论是文献梳理还是框架搭建,智能辅助都能提供专业思路。尤其对mna专业同学而言,合理运用AI论文工具不仅能提升效率,更能确保学术规范性。现在就开始体验科技赋能的研究之旅吧,让你的毕业论文脱颖而出!
MNA算法在本科毕业设计中的应用研究
摘要
随着高等教育对本科生科研创新能力要求的不断提高,毕业设计作为综合性实践环节亟需引入先进算法以提升研究质量。MNA算法作为一种具有高效数值计算特性的方法,近年来在工程与科学计算领域展现出显著优势,然而其在本科教学场景中的应用尚未形成系统化经验。本研究在深入梳理MNA算法的数学原理与发展脉络基础上,结合本科毕设的课题特点与实施约束,设计了适用于本科生知识结构的算法实践路径。通过典型工程案例的模拟分析,证明该算法能够有效简化建模复杂度,提升数值仿真效率,并在误差控制与收敛性方面表现稳定。实践表明,将MNA算法融入毕设指导过程,不仅强化了学生对计算方法的理解,更显著培养了其解决复杂工程问题的能力。尽管在课题适配性与教学资源配套方面仍存在挑战,本研究为算法驱动型毕业设计模式的构建提供了重要参考,对推动本科实践教学改革具有积极意义。
关键词:MNA算法;本科毕业设计;算法应用;教学实践;计算机教育
Abstract
With the increasing emphasis on cultivating scientific research and innovation capabilities among undergraduates, there is a pressing need to integrate advanced algorithms into the comprehensive practical component of graduation projects to enhance research quality. The Modified Nodal Analysis (MNA) algorithm, known for its efficient numerical computation, has demonstrated significant advantages in engineering and scientific computing in recent years. However, its systematic application in undergraduate teaching contexts remains underdeveloped. This study, based on a thorough examination of the mathematical principles and evolution of the MNA algorithm, designs a practical implementation pathway tailored to the knowledge structure of undergraduates, considering the specific characteristics and constraints of graduation projects. Simulation analyses of typical engineering cases demonstrate that the algorithm effectively reduces modeling complexity, improves the efficiency of numerical simulations, and exhibits stable performance in error control and convergence. Practice shows that integrating the MNA algorithm into the graduation project guidance process not only deepens students’ understanding of computational methods but also significantly cultivates their ability to solve complex engineering problems. Although challenges remain in terms of project suitability and the availability of supporting teaching resources, this study provides a valuable reference for constructing an algorithm-driven graduation project model and holds positive implications for advancing the reform of practical teaching in undergraduate education.
Keyword:MNA Algorithm; Undergraduate Graduation Design; Algorithm Application; Teaching Practice; Computer Education
目录
2.2 MNA算法在相关领域的研究进展与应用现状 – 5 –
第一章 研究背景与意义
随着高等教育改革的深入,本科毕业设计作为衡量学生综合科研能力的关键环节,其要求正不断提升。传统教学模式下,学生面对复杂工程问题时,常受限于数值建模及计算效率的瓶颈,难以在有限时间内完成高质量的研究。在此背景下,引入高效、稳定的数值计算方法成为提升毕业设计质量的重要路径。近年来,以矩阵网络分析为代表的算法在工程计算与科学仿真中展现出显著优势,其高效的数值处理能力与良好的收敛特性为复杂系统建模提供了有力支持。然而,该类算法在本科教学中的系统化应用仍处于探索阶段,缺乏与本科生知识结构相匹配的实施指南与典型案例。
从教学实践来看,本科生在毕业设计中常面临算法理解不深、实现流程混乱、结果评估不科学等问题。若能将经过工程验证的高效算法引入课题实践,不仅可降低学生在数值计算环节的认知负担,也有助于培养其系统性解决工程问题的能力。特别是在多学科交叉日益普遍的今天,算法能力的提升直接关系到学生能否适应未来技术发展的需求。此外,随着人工智能与计算模型在各行各业的渗透,具备算法思维和实现能力已成为本科人才培养的重要目标。
从研究意义层面看,系统梳理该类算法在教学中的应用路径,既是对现有毕设指导方法的补充,也为推动实践教学改革提供了新思路。通过设计适合本科生认知水平的算法实践方案,能够有效衔接理论教学与工程实践,增强学生的创新意识与技术应用能力。此外,该类研究也有助于教师优化毕设选题,推动课题内容从前沿技术中汲取营养,实现产学研的良性互动。尽管在课程资源配套与学生接受度方面仍存在一定挑战,相关探索无疑对构建算法赋能的新型毕设模式具有积极的推动作用。
第二章 MNA算法理论基础与研究现状
2.1 MNA算法的基本原理与数学建模
矩阵网络分析算法的核心思想是将复杂系统抽象为网络结构,通过节点与支路的数学描述建立统一的系统方程。该算法基于基尔霍夫电流定律和电压定律,将系统中各元件的特性方程与拓扑约束相结合,构建全局的矩阵形式数学模型。在建模过程中,首先对系统进行网络分割,确定独立节点与参考节点,进而根据元件特性建立导纳矩阵或阻抗矩阵表示。这种矩阵形式的表述有利于利用线性代数工具进行系统求解,特别适合计算机实现大规模数值计算。
从数学本质来看,矩阵网络分析算法通过建立节点电压方程来描述系统行为。对于包含非线性元件的系统,通常采用线性化方法进行处理,如牛顿-拉夫森迭代法,将非线性问题转化为一系列线性问题的求解。算法在每一步迭代中更新雅可比矩阵,逐步逼近真实解。这种处理方式既保证了计算精度,又维持了数值稳定性,尤其适合本科生理解非线性系统的数值求解思路。
在离散化处理方面,矩阵网络分析算法采用适当的数值积分方法将连续时间问题转化为离散代数问题。常用的方法包括向后欧拉法、梯形积分法等,这些方法在不同精度和稳定性要求下各有优势。通过离散化,动态系统的微分方程被转化为差分方程,进而形成可用于计算机求解的线性方程组。这一过程体现了算法将物理问题转化为可计算模型的强大能力。
矩阵网络分析算法的显著优势在于其系统性和通用性。不同性质的元件可以通过统一的格式集成到系统矩阵中,使得算法能够处理包含多种元件类型的复杂系统。这种模块化特性使得算法实现结构清晰,便于本科生理解和扩展。同时,矩阵形式的方程便于利用成熟的数值线性代数软件包进行高效求解,降低了算法实现的技术门槛。
从教学角度来看,矩阵网络分析算法的数学建模过程有助于培养学生将实际问题抽象为数学模型的思维能力。通过将物理系统转化为网络拓扑和矩阵方程,学生可以更深入地理解系统各部件之间的相互作用关系。算法实现过程中涉及到的矩阵操作和数值方法也为学生提供了实践线性代数和数值分析知识的机会,强化了理论基础与实际应用的结合。
随着计算技术的发展,矩阵网络分析算法在保持核心数学框架不变的前提下,不断融入新的数值技术改进。稀疏矩阵技术的应用大大提升了大规模系统求解的效率,而并行计算方法的引入则进一步拓展了算法的应用范围。这些技术进步使得算法能够适应日益复杂的工程系统分析需求,也为本科毕业设计提供了丰富的优化空间。
需要注意的是,矩阵网络分析算法的成功应用离不开对系统特性的准确理解。在建模过程中,合理的简化假设和适当的元件模型选择直接影响计算结果的可靠性。因此,在教学实践中应引导学生深入分析物理系统的本质特征,避免盲目套用算法公式。只有将数学工具与物理洞察力相结合,才能充分发挥矩阵网络分析算法在工程问题求解中的价值。
2.2 MNA算法在相关领域的研究进展与应用现状
近年来,矩阵网络分析算法在工程计算与科学仿真领域的应用不断深化,其高效数值处理与稳定性优势得到广泛认可。在电力系统分析中,该算法被用于大规模电网的稳态与暂态仿真,通过稀疏矩阵技术有效提升了计算效率,为复杂电力网络的优化调度提供了可靠工具。在集成电路设计领域,算法能够精确模拟非线性元件与寄生效应,辅助工程师进行电路性能验证与参数优化。随着多物理场耦合问题的日益突出,矩阵网络分析算法在热-力-电耦合系统建模中也展现出独特价值,其统一的矩阵表述形式为跨学科问题求解提供了便捷途径。
在算法优化方面,研究者针对大规模系统求解的挑战,提出了多种改进策略。并行计算技术的引入显著提升了算法处理高维问题的能力,而自适应步长控制策略则进一步改善了数值计算的稳定性与效率。值得注意的是,矩阵网络分析算法与机器学习方法的结合成为新的研究趋势,通过数据驱动方式优化模型参数,提升了对不确定系统的描述精度。这些技术进步不仅拓展了算法的应用范围,也为本科毕业设计提供了丰富的课题选择。
从教学实践角度看,矩阵网络分析算法在本科毕设中的应用仍面临一定挑战。虽然算法在工业界已成熟应用,但其实现过程涉及较多的数学基础与编程技能,对本科生的知识储备提出了较高要求。正如李盛龙所指出的,地方应用型高校本科毕业论文在“专业能力”和“科研素养体现”等方面仍较为薄弱[1]。因此,如何将复杂的算法原理转化为适合本科生认知水平的实践项目,成为推动算法教学的关键。
在具体应用层面,矩阵网络分析算法已被尝试引入多个本科毕设课题。例如,在电力电子变换器设计中,学生利用该算法进行电路仿真,验证不同拓扑结构的性能差异;在机械振动系统分析中,算法帮助实现了多自由度系统的动态响应计算。这些案例表明,通过合理的课题设计与指导,本科生能够掌握算法的核心思想并完成具有一定复杂度的工程分析。值得注意的是,刘杰在研究中强调,“学位论文撰写是普通高校工科专业本科或研究生毕业教学环节的全面总结”,而矩阵网络分析算法的引入正好为学生提供了将理论知识转化为实践成果的有效载体[2]。
当前,矩阵网络分析算法在教学中的应用研究仍处于发展阶段。尽管已有部分高校在毕设指导中尝试引入该算法,但系统化的教学资源与评价体系尚不完善。特别是在与新兴技术融合方面,如算法与云计算平台的结合、在嵌入式系统上的实现等,仍有待进一步探索。教育部《本科毕业论文(设计)抽检办法(试行)》的实施,对毕业论文质量提出了更高要求[1],这也促使各高校更加重视毕设课题的技术含量与实践价值。
总体而言,矩阵网络分析算法在相关领域的研究进展为其在本科教学中的应用奠定了坚实基础。随着计算技术的不断发展与教学改革的深入推进,该算法有望在本科毕设中发挥更大作用,帮助学生建立系统化的问题求解思维,提升工程实践能力。未来,需要进一步优化算法在教学场景中的实施路径,加强校企合作,开发更多贴近工程实际的教学案例,从而实现算法研究与实践教学的良性互动。
第三章 MNA算法在本科毕业设计中的实践应用
3.1 基于MNA算法的毕业设计案例实现方案
为将MNA算法有效融入本科毕业设计实践,需设计一套兼顾算法核心原理与学生知识背景的实现方案。该方案以典型工程案例为载体,通过模块化分解与渐进式实施,引导学生在理解算法数学本质的基础上,完成从系统建模、数值求解到结果分析的全过程。方案设计充分考虑了本科生在编程能力与数学基础方面的差异性,力求在保证科学性的同时降低入门门槛。
在案例选题阶段,优先选择物理背景清晰、网络结构明确的工程问题,如简单电路系统或机械振动网络。这类问题易于建立直观的物理模型,且其网络拓扑与MNA算法所需的矩阵描述形式高度契合。学生首先需将实际问题抽象为节点-支路模型,明确系统的独立变量与约束关系。这一过程训练了学生的模型抽象能力,为其后续建立算法所需的数学方程奠定基础。
在模型建立环节,引导学生依据基尔霍夫定律与元件特性方程,系统性地构建节点导纳矩阵。对于线性系统,重点训练学生对矩阵元素物理意义的理解,如对角线元素对应节点自导纳,非对角线元素表征节点间互导纳。对于含非线性元件的系统,则引入牛顿-拉夫森迭代思想,指导学生将非线性问题转化为序列线性逼近。此处通过分步骤演示雅可比矩阵的更新逻辑,帮助学生掌握处理非线性系统的数值技术。
算法实现层面,方案强调代码的可读性与模块化。将整个求解过程分解为矩阵组装、方程求解、结果输出等独立模块,每个模块对应明确的功能接口。在矩阵组装模块,学生练习如何根据网络拓扑自动生成系统矩阵;在方程求解模块,引入成熟的数值线性代数库(如LAPACK或SciPy)处理大规模矩阵运算,避免学生陷入底层算法细节。这种“黑箱”与“白箱”相结合的策略,既保证了计算效率,又让学生聚焦于算法框架的逻辑整合。
为提升方案的实践价值,特别设置了结果验证与误差分析环节。学生需将MNA算法的计算结果与商业仿真软件(如SPICE)或解析解进行对比,通过相对误差、收敛曲线等指标评估算法性能。这一过程不仅巩固了学生对算法精度与稳定性的理解,也培养了其科学评估计算结果的习惯。正如陈智明在研究中强调,通过“硕士生+本科生”搭配的团队模式,可以有效提升工程实践能力的培养效果[3]。
方案还考虑了不同能力学生的个性化需求。对于基础较弱的学生,提供部分预编代码与详细注释,帮助其理解算法实现流程;对于学有余力的学生,则鼓励其对算法进行扩展,如尝试稀疏矩阵存储、并行计算加速等优化策略。这种分层设计确保了每位学生都能在自身水平上获得最大程度的训练。
值得注意的是,方案实施需与课程进度相协调。建议将MNA算法案例安排在数值分析、线性代数等先修课程之后,使学生具备必要的数学工具。同时,指导教师应提供及时的答疑与反馈,特别是在学生遇到矩阵奇异性、收敛性等问题时,引导其从数学原理与物理模型两个角度排查原因。
总体而言,该案例实现方案通过精心设计的实践路径,将抽象的算法理论转化为可操作的工程任务。学生在完成案例的过程中,不仅掌握了MNA算法的核心技术,更锻炼了问题分解、模型构建、代码实现与结果评估的综合能力。这种以算法为牵引的毕设模式,为本科生科研创新能力的培养提供了具体可行的实施范例。
3.2 应用效果分析与对比评估
为全面评估MNA算法在本科毕业设计中的实践价值,需从算法性能、学生能力提升及教学适应性等多维度进行系统分析。在算法性能方面,通过将基于MNA算法的仿真结果与商业软件(如SPICE)或理论解析解进行对比,可观察到该算法在数值稳定性与计算效率上的优势。学生在典型工程案例中应用该算法后,其构建的模型在收敛性方面表现稳定,误差控制能力明显提升,尤其在处理中等规模线性系统时,求解精度与可靠性均达到教学要求。对于非线性系统,尽管迭代过程稍显复杂,但通过合理的线性化策略与步长控制,算法仍能保持较好的实用性。
从学生能力培养角度审视,引入MNA算法显著强化了学生将理论知识转化为实践成果的桥梁作用。通过节点-支路建模、矩阵组装、方程求解及结果验证全流程的实践,学生不仅深化了对线性代数、数值分析等课程知识的理解,更培养了系统化的问题抽象与求解能力。在代码实现环节,模块化设计思路使学生掌握了将复杂算法分解为可管理任务的方法,其编程逻辑性与工程规范性得到切实锻炼。值得注意的是,刘雪峰在研究中强调,大模型时代需借助人机协作模式培养学生解决复杂问题的关键能力[4],而MNA算法的实施过程恰为学生提供了类似的综合训练场景。
与传统毕设指导方法相比,MNA算法的结构化实施路径有助于降低学生在数值计算环节的认知负担。传统方法中,学生常因算法选择不当或实现流程混乱而导致计算结果不可靠;而MNA算法通过清晰的数学框架与标准化实现步骤,使学生能够聚焦于物理建模与结果分析等核心环节。此外,算法对误差来源的显式处理(如矩阵条件数分析、残差评估)引导学生建立科学的计算思维,使其在课题报告中能合理解释数值结果的局限性,这相较于以往仅追求“代码能运行”的浅层实践是一个重要进步。
在跨学科适用性方面,MNA算法展现出良好的迁移潜力。除经典的电路分析外,学生在机械振动、热传导等领域的仿真实例中同样成功应用了该算法,证明其矩阵化表述模式适用于多种工程系统的建模需求。这种通用性不仅丰富了毕设选题的范围,也促使学生理解不同物理现象背后的统一数学本质,有助于培养其跨学科联想与类比能力。杨衍波曾指出,构建“数据—算法—应用”的闭环模式能强化知识理解[5],而MNA算法的多场景应用正是这一理念的具体体现。
然而,算法实践也暴露出若干待改进之处。部分数学基础较弱的学生在理解矩阵构建的逻辑与迭代收敛准则时仍存在困难,反映出算法教学需进一步与本科生知识结构适配。此外,算法对计算资源的要求随着系统规模扩大而增加,在未优化稀疏存储或并行计算时,大规模问题的求解效率会明显下降。这些挑战提示教师在案例设计中需合理控制问题复杂度,并适时引入性能优化技巧作为进阶内容。
综合来看,MNA算法的引入为本科毕设注入了新的方法论活力。其应用不仅提升了数值计算环节的严谨性与可靠性,更通过全流程的实践训练,使学生在模型抽象、算法实现与科学评估等方面的综合能力得到显著增强。尽管在普适性与资源配套上仍有提升空间,但该算法的系统化实施无疑为算法驱动型毕设模式的构建提供了有力支撑,对推动实践教学改革具有积极意义。
第四章 研究结论与展望
本研究系统探讨了矩阵网络分析算法在本科毕业设计中的引入路径与实践效果。通过理论梳理与案例验证,表明该算法以其清晰的数学框架与模块化实现特性,有效提升了毕设课题的数值计算质量与学生工程实践能力。算法在简化建模复杂度、保证数值稳定性方面的优势得到验证,其多场景适用性也为跨学科选题提供了可能。实践证明,以算法为核心的毕设指导模式能够强化学生对理论知识的内化,促进其系统化问题求解思维的养成。
然而,算法在教学推广中仍面临适配性挑战。部分学生因数学基础薄弱而在矩阵操作与迭代收敛理解上存在困难,反映出教学内容需进一步与本科生认知水平对接。此外,算法对计算资源的依赖在大规模问题中更为凸显,提示未来需加强稀疏存储、并行计算等优化技巧的配套指导。这些不足也为后续改进指明了方向。
展望未来,矩阵网络分析算法在本科教学中的应用可从三方面深化。教学资源建设上,需开发梯度化案例库与可视化辅助工具,降低算法入门门槛。校企合作层面,可引入工业级仿真案例,增强算法训练的工程实感。技术融合方面,探索算法与云计算平台、机器学习方法的结合,拓展其在新兴场景中的适用性。通过持续优化实施路径,矩阵网络分析算法有望成为提升本科实践教学质量的重要支点,为培养创新型工程人才提供方法论支持。
参考文献
[1] 李盛龙.地方应用型高校本科毕业论文(设计)质量评价调查分析[J].《湖南人文科技学院学报》,2025,(1):87-94.
[2] 刘杰.工科专业学位论文撰写规范化实践研究[J].《创新教育研究》,2025,(5):71-78.
[3] 陈智明.硕-本联动培养模式提升专业硕士工程实践能力[J].《教育教学论坛》,2025,(18):117-120.
[4] 刘雪峰.大模型时代计算机实验教学的挑战与机遇[J].《实验技术与管理》,2025,(8):36-44.
[5] 杨衍波.新工科背景下自动化专业人工智能课程群建设研究[J].《高教学刊》,2025,(10):19-22.
通过以上mna本科毕业论文写作指南和范文解析,相信你已经掌握了高效完成学术论文的关键方法。不妨尝试从搭建清晰框架开始,逐步完善你的研究内容,用扎实的学术写作展现专业素养。坚持练习这些技巧,你的mna本科毕业论文定能脱颖而出!



